通过知识蒸馏实现的隐式思维链推理 [译]
Yuntian Deng*1,2 Kiran Prasad3 Roland Fernandez3 Paul Smolensky3,4
Vishrav Chaudhary3 Stuart Shieber1
1 哈佛大学 2 艾伦人工智能研究所 3Microsoft
4 约翰霍普金斯大学
摘要
为了让语言模型具备推理能力,研究人员通常会通过特定提示或调整模型使其在给出最终答案前,先产出一连串的推理步骤。不过,人类虽然能够用自然语言有效推理,可能对于语言模型来说,使用一些非自然语言形式的中间运算步骤,推理会更加高效。在本项研究中,我们探索了一种不同于传统的推理方式:不是直接输出每个推理步骤,而是通过语言模型内部的隐藏状态进行隐式推理。这种隐式的推理步骤,是通过对一个接受过显式思维链推理训练的教师模型进行“知识蒸馏”得来的。不同于传统的“横向”逐字输出推理过程,我们的方法是“纵向”的,在模型不同层级的隐藏状态间进行推理。通过对多位数乘法任务和小学数学问题数据集的实验,我们发现这种方法能解决那些没有显式思维链条就无法解决的问题,并且其速度与直接给出答案而不进行任何推理的速度相当。
1 引言
大语言模型在处理需要深入语言理解和逻辑推理的任务时展现了卓越的能力,这些任务包括进行多步骤的问答(Yang et al., 2018;Yao et al., 2023b)和解数学题(Hendrycks et al., 2021;Cobbe et al., 2021;Welleck et al., 2022;Wei et al., 2022b;Kojima et al., 2022;Chen et al., 2022;Yue et al., 2023;Chern et al., 2023)。为了引出它们的推理能力,现有一个普遍采用的方法叫做链式思考推理。在这种方法中,模型会被训练或引导去详细阐述解决问题的中间步骤,然后给出最终答案。
尽管这种做法与人脑解题的方式不谋而合,但它可能尚未充分发挥出语言模型的计算能力。来看看 transformer 架构(Vaswani 等人,2017)吧,它能够在“横向”上逐个单词地产生文本,在“纵向”上通过许多层的内部隐藏状态来处理信息。以 GPT-3 为例,它有高达 96 层(Brown 等人,2020),我们不禁要问:为什么不让模型通过它们的层级“纵向”进行内部推理,而不是非要逐步阐释每一个中间环节来得出解答呢?这样不仅可以大幅节约在生成思维过程链时所需的大量时间,还可能让模型开发出更高效的推理方法,这些方法可能不那么易于人类理解,但却不受人类思维模式的束缚。
虽然思维过程链(CoT)方法已经取得了显著的成果,但在产出最终答案的过程中生成 CoT 本身却有所拖延。因此,值得研究是否能将 CoT 方法的见解应用于能够直接给出答案的模型。我们从人脑将显性、有意识、深思熟虑的推理(系统 2)转化为更隐性、自动、直觉思考(系统 1)的过程中汲取灵感(Anderson,2005;Kahneman,2011),寻找一种方法,将显性的 CoT 推理编译进一个能够直接输出最终答案的模型中。我们称这种方法为隐性思维过程链。具体操作上,我们会取出一个专门训练用来生成 CoT 的教师模型在推理过程中产生的跨 transformer 层的内部状态,并训练另一个模型来预测这一系列状态的压缩编码;然后,在推断阶段,利用这个预测状态序列为一个学生模型提供额外信息,帮助其直接产出最终答案。也就是说,我们将在显性 CoT 模型中横向自回归生成的内部状态转换为预测的纵向状态序列,用以直接输出答案,用隐性的(垂直)推理取代了(横向的)显性 CoT 中的推理。
在传统的连锁推理 (CoT) 训练中,通常采用“教师指导法”来指导模型一步步生成推理过程。而在我们的新方法中,我们不再用这种强制性的手段,而是让一种先进的模型(教师模型)来指导另一个模型学习它产生思维链时的内部机制:这可以看作是“教师教学”,而不是简单的指令传达。
我们的策略可以分为三个步骤:
- 解读教师心思:我们培养一个学生模型去“解读”教师的思维过程,也就是在推理过程中教师模型内部的连续隐藏状态。这个学生模型不是简单模仿,而是利用这些隐藏状态来得出答案。\
- 思维模拟:接下来,我们使用知识蒸馏技术(Hinton 等人,2015; Kim 和 Rush,2016),培训一个能够预测教师隐藏状态的模拟器。这样做可以直接跨越多个处理层次,无需再走教师推理的每一步。\
- 结合优化:最后,我们将这个能够预测教师思考过程的模拟器与能够根据这个模拟过程给出最终答案的学生模型结合在一起。然后我们对整个系统进行端到端的优化,让学生模型能够发展出与教师不同的推理方式。
我们的实验结果展现了隐式思维链推理的巨大潜力。在进行多位数乘法的合成任务中,尽管标准训练方式无法在缺乏明确推理步骤的情况下给出最终答案(甚至 GPT-4 在处理五位数乘以五位数的问题时也会遇到挑战),但我们的方法让一个 GPT-2 Medium 模型能够直接解决多达五位数的乘法问题。此外,在解决真实世界的小学数学问题时,我们的方法能在 GSM8k 上获得 22% 的准确率,而这一切都不需要明确的推理步骤。
我们工作的主要贡献包括:首先,我们证明了从“教师指导法”到“教师教学法”的转变能够加快答案生成的速度;其次,我们展示了如何将教师的明确推理过程蒸馏成学生的隐式推理能力;最后,我们证明了通过结合前两点,可以直接生成数学问题答案的性能得到了显著提升。我们的代码、数据和预先训练好的模型可以在以下网址找到:https://github.com/da03/implicit_chain_of_thought/。
2 显性、隐性及无思维链条推理
想象一下,有一项任务需要通过几个步骤来逐步推导出结果。假定 是我们的问题, 是解题过程中的中间步骤,而 就是我们要找的答案。比如说,在解一个乘法题 , 就是问题本身 , 可能是把这个问题分解成 的过程(这样就把乘法分解成了我们能看见的步骤),而 就是最后的答案 。对于这类任务,我们训练模型的目的是要弄清楚在已知 的情况下,输出 的概率分布 。解决这类问题,大体上有三种方法:不使用思维链条的推理(No CoT),使用显性思维链条的推理(Explicit CoT),和使用隐性思维链条的推理(Implicit CoT)。
2.1 不运用连贯思维推理
在这个方式中,模型仅仅通过输入 来直接输出结果 ,而不涉及任何中间步骤 。用数学的语言来说,就是直接用模型 来定义从输入到输出的关系,并且通过成对的输入输出 进行训练。拿 这个乘法为例,模型会直接得出答案 ,正如 表 1 所展示的“无连贯思维推理(CoT)”一栏。这种直接解决问题的方式对简单任务来说是可行的,但是对于复杂的问题,让模型在没有任何中间步骤的引导下自行找出答案,就像让学生在不了解计算过程的情况下学习多位数乘法一样,难度非常大。
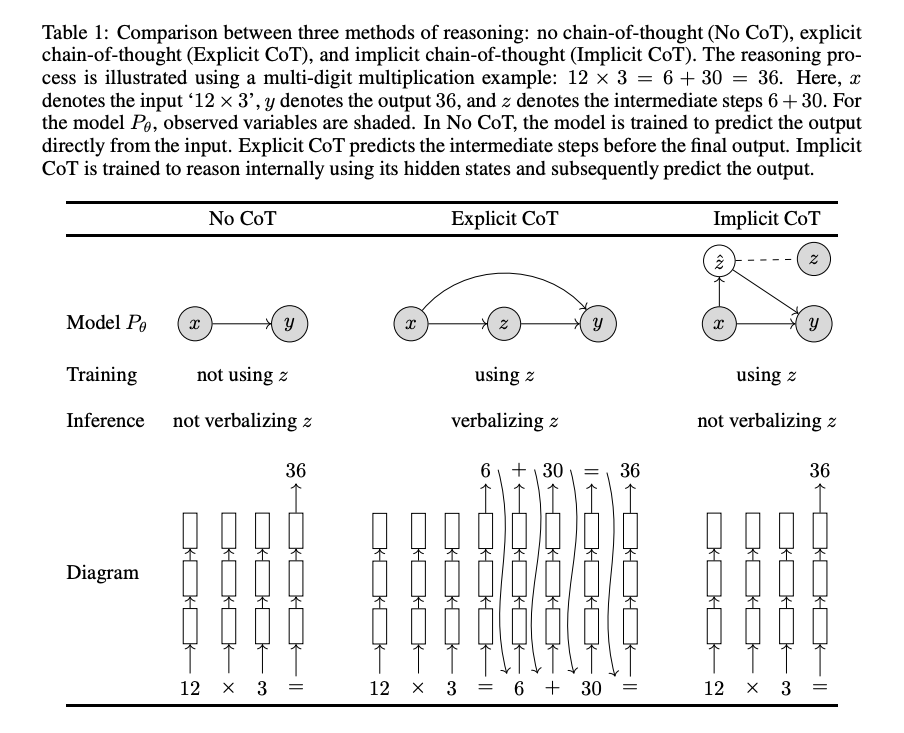
表 1: 对比无思维链路(No CoT)、显式思维链路(Explicit CoT)和隐式思维链路(Implicit CoT)三种推理方法。以一个多位数乘法为例来展示推理过程:。这里, 代表输入‘’, 代表输出结果, 代表中间计算步骤。在模型 中,已观察到的变量被标记出来。在无思维链路方法中,模型直接从输入学习预测输出。而显式思维链路方法先预测中间步骤再得出最终输出。隐式思维链路则通过训练模型内部隐藏的状态来推理,然后预测输出结果。
2.2 显式思维链推理
在显式思维链推理的方法中(Nye et al., 2021; Wei et al., 2022b),模型被训练以首先明确产出中间步骤,然后再给出最终的结果。它不只是简单地模拟从输入到输出的过程,而是考虑到输入和输出之间的联合概率分布,并通过计算来细致地分析这个过程。
2.3 潜在思路推演
隐式链式思维推理是一种坐落于两种极端方法之间的推理方式。在模型训练时,它会接触到一些中间步骤,用 表示,但在测试阶段,模型不会明显地呈现这些步骤。它将这些步骤内化在内部状态中,用 标记,进而输出最终结果 。用更正式的数学语言表达,就是 。这个过程就像人们在完全吸收了某个概念之后,常常可以跳过显性的逻辑推理,直接得出结论。例如,在我们之前的乘法例题中,模型会直接给出 的答案为 ,因为它已经在内部完成了计算步骤。这种推理的示意图与不使用链式思维推理的示意图一样,可以在 表 1 的“隐式 CoT”部分找到。

图 1: 隐式思维链推理的三步策略。 (a) 读心术教师:学生模型通过“读取”教师模型的连续隐藏状态(内部推理过程),利用这些信息产出答案。(b) 思维模仿:通过给定的输入,训练一个模仿器来预测教师的隐藏状态,这样做可以模拟教师的内部推理过程,而无需明确列出每一步的推理。(c) 结合与优化:将模仿器与读心学生模型整合,形成一个联合系统。随后对这个系统进行端到端的微调,使学生模型能够形成自己的推理路径,这可能与教师的原始方法有所不同。
3 实施隐式思维链推理的方法
我们提出了一套三步走策略来实现隐式的思维链推理,这一策略基于一个经过训练、专门进行明确的横向思维链推理的教师模型。第一步,我们训练学生模型仅使用教师模型中的隐藏状态(这些状态包含中间推理步骤的信息)来生成答案,这样学生就能直接从问题输入和教师提供的线索中得出结论,而不需外显的推理步骤,我们称这个过程为“读心术教师”。第二步,我们通过知识蒸馏训练一个仿真器,它能从问题中垂直推理出教师的隐藏状态,这一步我们称为“思维模仿”。最后一步,我们把学生模型和仿真器结合起来,学生模型会利用仿真器预测出来的教师状态来得出最终的答案。然后我们对这个整合后的模型进行端到端的精调,以此来优化其内部的推理过程,我们把这一步骤称为“结合与优化”。所有这些步骤都在 图 1 中展示。
在概述了这套方法之后,我们进一步探究了在使用变压器架构(Vaswani 等人,2017)来构建我们的教师模型、学生模型和仿真器时的具体实施细节。变压器的分层处理能力为我们垂直推理的概念提供了理想的实施平台。
3.1 破解教师的思维密码
当老师开始处理信息、进行逐步推理并给出结果时,他们脑中隐藏的思维状态就像是捉迷藏的信息一样,与特定的 token 紧密相关。比如说,在一个由 层构成、并处理 个中间 token 的 transformer 模型中,这些神秘的思维状态就被编码在一个 维的二维矩阵 中,矩阵中的每个元素 都代表了在第 层时对应于第 个中间 token 的隐藏状态。
信息提取技巧
为了简化问题,我们首先假设 。在这个 向量矩阵中,我们尝试只选出 个向量,这样一个层数对等的仿真器就可以试着每层预测一个向量。实验告诉我们,直接从矩阵中挑出对角线上的元素是个不错的办法。直观上来讲,预测 对仿真器来说是小菜一碟,因为此时只涉及一个中间 token。随着对角线的推进,从 到 ,我们就像是在逐渐增加难题的级别,逐步加入更多的中间 token 和层次,直到 ,它包含的信息量应该足够老师开始给出答案了。
应对变化的思维链条
在真实场景中,我们可能会遇到变化的中间 token 数量,这导致列数 的不确定性。为了应对这种情况,我们设置了一个超参数 ,通过均匀选取列(大概每隔 列取一个)来解决问题,同时保持每行选取一个向量。选择的第 个向量是 ,其选择依据如下表格所示:
在实验中,我们不仅试验了固定 值的效果,还有一个根据每个实例中的中间 token 数量 动态调整的 值 ,这都是基于实验的验证性能来决定的。
学生模型训练
我们训练的学生模型层数与其老师(即先进模型)相同。在抽取了 L 个向量之后,这些向量会取代学生模型初始输入后的隐藏状态。想要直观了解这个过程,请参考 图 0(a)。然后我们训练学生模型去预测最终的答案,而教师模型在此过程中保持不变。
3.2 思维仿真
在实际测试中,学生模型不能使用教师模型筛选出的 L 个向量 ,所以我们必须训练一个仿真器,让它能够直接从输入数据预测这些向量。我们训练了一个与教师层数相同的仿真器,它需要在处理输入数据后,预测出每一层对应的单个向量 ,如 图 0(b) 所展示的。我们通过最小化平均平方误差来对这个仿真器进行训练:
多条推理途径
当有多条可能的推理途径存在时,使用均方误差来匹配教师的思考状态往往无法得出准确的预测结果。这好比用一个简单的高斯分布去适应一个复杂的高斯混合模型,结果仅能找到其中心位置。例如,设想这样一个小学数学题:Asumi 有 30 本历史书,25 本文学书。请问 Asumi 一共有多少本书? 解题过程中可能会有两个步骤:(1) 或者 (2) ,这对应两种不同的可能状态 和 。如果运用 方程 1 所示的方法,理想的解会是 ,但这并不代表任何一个实际的推理路径。因为模拟器只能获取输入 的信息,它无法辨别两种情况。
为了处理多种推理途径,我们不再预测每一层的单一状态 ,而是预测多个可能状态的混合 ,这样每个混合部分 就能表示教师思考状态分布的不同方面。
为了给这个分布建模,在 层,我们假设模拟器的隐藏状态为 。我们定义每个混合部分的分布 为一个以 和 为参数的高斯分布 ,并将混合部分的分布 定义为一个以 和 为参数的分类分布 。
在实践中,我们发现,试图直接构建这种混合模型往往会导致模式崩塌(参见 He 等人,2019)的问题,这种情况下,模型只倾向于使用极少数的混合成分。为了改善这个状况,我们采用了一种方法:使用中间步骤的代号 44 在这里,不加粗的 指代中间代号。我们将这个代号定位在 ,并指导分类器 与它匹配。我们的最终目标公式如下:
例如,在第一层(即 ,)的情形下,如果是情况(1),我们会让混合组件 对应数字“30”,并且调整 以适配 ;而在情况(2),我们会指定 为“25”,并调整 以配合 。这样,两个不同的情况就对应着不同的混合组件。
3.3 结合并优化
如今,我们可以将模拟器预测的教师状态 提供给那个具有心灵感应能力的学生模型,并且通过最大化最终产出的概率来全面优化整个系统。值得注意的是,在学习过程中,整个系统的内部推理过程可能会与教师模型的原始方法出现偏离。而且,这个步骤不需要中间推理步骤的训练数据。
就混合模型而言,我们本希望通过选取最大概率的推理路径——即 的 argmax ——来实现,但这一运算并不是完全可微分的。作为替代,我们采用了一个温度较低的 softmax 函数来近似实现 argmax,这是一个完全可微分的过程。详情请参阅附录 D。
4 实验设置
4.1 数据
我们针对两项任务展开了实验:首先是 BIG-bench 基准测试中的多位数乘法任务(作者,2023;Suzgun 等人,2023),这被认为是算术任务里面难度最大的一项(Yang 等人,2023)。我们特别关注了四位数()和五位数()乘法问题,因为在不采用 CoT 的情况下,解决这两种问题非常有挑战性。第二个任务是解决小学数学题,这需要理解语言和数学推理的能力。我们选用了 GSM8K 数据集(Cobbe 等人,2021)进行研究。
中间推理步骤
在解决乘法问题时,我们会将问题分解为一步步的计算,即将被乘数与乘数的每一位分别相乘,同时记录下每个部分乘积和部分总和。在 GSM8K 数据集的实验中,我们遵循 Wei 等人在 2022b 年的方法,使用自然语言描述的中间步骤来明确展示 CoT。在训练隐式 CoT 的导师模型时,为了尽可能减少 transformer 层与中间步骤数量之间的差异,我们仅保留了方程式。
数据增强的实验
在我们早期的尝试中,我们注意到,与传统的预训练语言模型不同,我们推出的隐式 CoT(Chain of Thought)技术需要大量的训练数据。因此,为了满足这一需求,我们制作了两个任务的合成数据。
在进行多位数乘法运算的任务中,我们专门选取了与 BIG-bench 数据集不重叠的公式。而在 GSM8K 任务上,我们利用 GPT-4 (OpenAI, 2023) 创造了 40 万个新的数学题目,这些题目的格式与 GSM8K 保持一致。之后,我们对这些题目进行了筛选,清洁,并且将这个数据集命名为 GSM8K-Aug。需要指出的是,对于这两个任务,我们并没有修改原始测试集。增强后数据集的详细统计在 表 2 中有展示,从中我们可以看出,使用显式 CoT 后,生成的 token 数量激增了 5 到 30 倍。想了解更多数据细节,请参阅 附录 A。
| 数据集 | 原始大小 | 增强后大小 | #输入 Token | #中间 Token | #输出 Token |
|---|---|---|---|---|---|
| Mult | 0 | 808k | 9 | 47 | 9 |
| Mult | 0 | 808k | 11 | 75 | 11 |
| GSM8K-Aug | 7k | 378k | 51 | 59 | 2 |
表 2: 数据集统计信息。这里的“大小”是指训练集的规模。输入、中间、输出 Token 的数量是根据验证集来的中值数据。Token 数量是根据 GPT-2 的 token 制器计算的,并且对中间和输出 Token,都包含了一个特殊的结束符号。
4.2 比较基准
我们把我们的方法与不使用 CoT 以及使用显式 CoT 的方法做了比较。具体来说,我们比较了在增强训练数据集上进行微调后的 GPT-2 Small、GPT-2 Medium、GPT-2 Large,以及在少次样本提示(few-shot prompting)条件下的 ChatGPT 和 GPT-4,详见 附录 C。
4.3 模型介绍
在探索隐式的 CoT 方法时,我们对较小和中等大小的 GPT-2 模型进行了微调。为了确保模型训练的稳定性,我们对教师模型的对角状态做了规范化处理,将其转换为零均值且标准偏差为一,类似于应用了没有可训练参数的层规范化技术(Ba 等,2016)。我们观察到,高层的隐藏状态通常具有更大的范数。在“读懂教师思维”这一步骤中,我们在教师状态之上增加了一个可训练的单层 MLP,以便能够进行信息的复制。在“模仿思维”这一步骤,我们引入了一个带有自我关注机制的 LSTM 网络(Hochreiter 和 Schmidhuber,1997),用于在预测教师状态前处理垂直隐藏状态。至于混合模型部分,我们在仿真器的隐藏状态上叠加了一个线性映射层,用以预测不同混合组分的分布,并通过将隐藏状态 与混合组分嵌入 结合后,使用单层 MLP 进行处理以计算 。
在 GSM8K-Aug 项目中,我们采纳了这种混合策略,但并未在乘法问题中应用,因为在乘法问题中,中间步骤由输入唯一决定,不存在多样性。在混合策略中,我们在“结合并优化”阶段设置了 0.05 的“温度”参数。欲了解模型的全部详细信息,请查阅附录 D。
| 模型 | #层 | 乘法操作 | 乘法操作 | GSM8K-Aug 拓展 | |||
|---|---|---|---|---|---|---|---|
| 准确率 | 吞吐量 | 准确率 | 吞吐量 | 准确率 | 吞吐量 | ||
| 无链式转换 (CoT) | |||||||
| GPT-2 小模型 | 12 | 0.29 | 1.00 | 0.01 | 1.00 | 0.13 | 1.00 |
| GPT-2 中模型 | 24 | 0.76 | 1.00 | 0.02 | 1.00 | 0.17 | 1.00 |
| GPT-2 大模型 | 36 | 0.34 | 1.00 | 0.01 | 1.00 | 0.13 | 1.00 |
| 隐式链式转换 (CoT) | |||||||
| GPT-2 小模型 | 12 | 0.97 | 0.67 | 0.10 | 0.71 | 0.20 | 0.66 |
| GPT-2 中模型 | 24 | 0.96 | 0.69 | 0.96 | 0.73 | 0.22 | 0.66 |
| 显式链式转换 (CoT) | |||||||
| GPT-2 小模型 | 12 | 1.00 | 0.17 | 1.00 | 0.14 | 0.41 | 0.08 |
| GPT-2 中模型 | 24 | 1.00 | 0.17 | 1.00 | 0.14 | 0.44 | 0.08 |
| GPT-2 大模型 | 36 | 1.00 | 0.17 | 0.99 | 0.15 | 0.45 | 0.08 |
表 3: 主要研究结果一览。准确率(Acc)用来衡量预测结果与正确答案完全一致的比率。吞吐量则指在单批次处理下,每秒可以处理的样本数量,并以无链式转换(CoT)模型的吞吐量作为基准进行了归一化处理。
5 结果
表 3 显示了我们的研究成果。与没有使用 Chain of Thought(CoT)技术相比,我们的方法能够解决以前无法仅通过直接推理解决的问题:比如,在不使用 CoT 的情况下,GPT-2 中型模型在解决 乘法问题时的正确率仅为 2%,但在应用了隐式 CoT 之后,正确率飙升至 96%。同样地,在 GSM8K-Aug 数据集上,隐式 CoT 实现了 22% 的直接解题准确率,相较于不使用 CoT 的 GPT-2 最佳模型仅有 17% 的准确率。
有意思的是,在隐式 CoT 的帮助下,GPT-2 小型模型在解决 乘法问题时表现出色,准确率达到了 97%。但是,当问题升级到 乘法时,其正确率骤降至 10%,而 GPT-2 中型模型却能保持 96% 的高准确率。这似乎说明,隐式 CoT 的有效性可能与模型足够的层级数对于中间计算的要求有关。
如果与明确指出思路的 CoT 相比,隐式 CoT 相对落后很多,这可能有两个原因:一是我们使用的基础语言模型都是针对水平推理进行预训练的;二是我们实验中使用的层数(GPT-2 中型为 24 层)可能还不够支持需要的推理步骤。尽管如此,隐式 CoT 在推理速度上具有明显优势,特别是在 GSM8K-Aug 数据集和 乘法这种涉及多个中间步骤的任务上。例如,在 GPT-2 中型模型上进行 乘法计算时,隐式 CoT 的速度是没有使用 CoT 的情况的 73%,而明确的 CoT 方法的速度仅为 14%。这是因为隐式 CoT 直接输出最终答案,唯一的时间消耗来自于可以理论上并行化(尽管我们的实验中没有这样做)的模拟器。
6 分析
把不同的子集作为老师的思维过程
在我们的主要实验中,我们选择了教师隐藏状态矩阵的对角线元素。我们尝试了其他几种压缩编码方法,但效果并不理想。以 GPT-2 小型模型进行的 乘法任务为例,当选用对角线元素时,我们达到了 100.0% 的验证准确率;而选择第一列时准确率下降到 29.9%;选用顶行时能达到 84.4%;底行的结果则是 57.6%。
混合手段的必要性
在 GSM8K-Aug 问题集中,因为有许多不同的解题路径可以选择,所以混合手段变得尤为关键。如果不运用混合手段,我们使用 GPT-2 Small 模型在这个增强集上的验证准确率仅为 11.2% (设置 )。但是当引入混合手段后,准确率显著提高到了 20.2%。
耦合过程与优化策略
在此过程中,“优化”环节同样不容忽视。在 GSM8K-Aug 数据集上,如果我们仅仅是把 GPT-2 Medium 模型和用于推理的学生模型结合起来,不做进一步优化,那么验证准确率将停留在 9.4%。但是,如果进行了深入优化,准确率能够飙升至 21.9%。让模型自主形成推理路径也是至关重要的:如果我们只对学生模型进行优化,而不更新仿真器模型,准确率则会降至 13.0%。
在混合手段中,我们引导模型将混合组件设定为与当前中间令牌一致,这样我们就能把预测出来的混合组件对应回实际的单词。在进行“优化”操作之前,这些对应回的单词与老师在 设置下的中间推理步骤非常相似,如果直接用这些单词来预测答案,准确率可以达到 9.4%。然而,经过“优化”操作后,预测出的混合组件失去了原有的可理解性,这一点在 附录 F 中的 表 5 有详细展示。
7 相关研究
新兴能力
最新研究发现,只要优化得当,语言模型就能够解决基础算术问题(Power 等,2022)。对于那些需要多步逻辑推理的任务,只要提升模型的规模和数据量,就能显著提高模型的直接解题能力。举个例子,Wei 等人(2022a)发现,在 GSM8K 数据集上(未使用 CoT 方法),随着训练所使用的浮点运算次数从 提升至 ,测试的准确率可以从不足 5% 提高到大约 7%。另有研究(Yang 等人,2023)通过对一个 20 亿参数的语言模型进行训练,使用了 5000 万个训练样本通过课程学习,使其在解决 乘法问题上的准确率达到了 89.9%。这些研究结果表明,只要模型规模足够大,它就能够内部进行多步推理。我们的方法与众不同,因为我们使用了教师模型的思维过程,以更高效的方式训练模型。
知识传递
我们所说的“思维模拟”实际上是一种知识传递方法,在这个过程中,教师模型将它的知识传递给学生模型(Hinton 等,2015)。这种技术传统上用于压缩模型体积(Kim 和 Rush,2016)或用于非自回归机器翻译(Gu 等,2018)。在我们的实践中,这种方法用于将教师模型的横向推理方式转化为模拟器和学生模型的纵向推理方式。
8 局限性
缺乏透明度和可解释性
显式的连续输出(CoT)因其透明性而备受青睐:通过中间步骤,可以轻松理解模型是如何推理的。而隐式的 CoT 因为其处理过程隐藏在内部状态中,从而缺少这种透明度。尽管这种方法在生成过程中更加紧凑、高效,但它牺牲了人类的解释能力,让人们难以理解模型是如何得出最终结论的。
借鉴导师的思维方式
在我们目前的三步战略中,大致上我们在尝试将教师模型的“横向思维”精华转化到学生和模拟器的“纵向思维”中。虽然隐性推理的宏伟蓝图旨在培养模型自主形成独到的推理路径,但我们的初步尝试还是不得不大量借鉴导师的思考方式作为我们的起点。
表现上的落差
目前我们在隐性思维连续尝试(CoT)上的成果还没有显性思维连续尝试来得出色。不过,这只是构建隐性思维连续尝试之旅的第一步,我们相信未来还有很大的改进和提升空间。
9 总结及展望
在本研究中,我们推出了一种新概念——对于基于变换器的语言模型来说,推理可以在隐藏层“垂直”进行,而不是传统的“水平”方式,即通过生成步骤性的中间代币来完成。这种方式让模型有可能不再局限于模仿人类的推理方式,而是形成一套独特的内部推理机制。
要应用这一理念,我们设计了三步走策略:‘心灵感应’老师,模拟思维过程,以及耦合与优化。核心思想是将一位专注于传统水平推理的‘老师’模型的知识,传授给专门训练进行‘垂直’推理的‘学生’和模拟器。通过在数学乘法和小学数学问题的实验中可以看出,这种方法大大提升了直接给出答案时的性能——尽管明确地展示推理链条可以更大幅度地提高答案准确性。
我们期待在这项工作的基础上探索更多令人激动的新方向。比如,未来可以尝试使用变分自编码器(Kingma 和 Welling,2022)进行全面的端到端联合训练,把模型的内部推理过程当作一个潜在的未观察变量来处理。还可以尝试采用能够处理多峰分布的图像建模技术,如扩散方法(Sohl-Dickstein et al., 2015; Ho et al., 2020; Song et al., 2021)来训练模拟思维过程。此外,还可以探讨把这种新方法融入预训练阶段,让语言模型不仅能够执行水平的显式推理,还能够进行垂直的隐式推理,克服现有模型在无法进行显式推理时性能大幅降低的问题。
10 鸣谢
YD 的研究由 Nvidia 奖学金资助。我们还要对哈佛大学 FAS 研究计算部门提供的计算资源表示感谢。
附录 A 数据增强与处理
A.1 多位数乘法解析
在处理多位数乘法问题时,我们首先随机选择两个多位数字作为例子,然后计算它们的乘积。经过筛选去除重复项之后,我们准备了 808,000 条用于训练的方程式以及 1,000 条用于验证的方程式。我们选取 BIG-bench 数据集作为测试用例。为了详细演示计算过程的每一步,我们把这个问题细分成了多个单一数字与被乘数相乘的步骤,并记录下每一步的乘积和累加和。为了让计算过程更加直观,我们把数字序列颠倒过来,让个位数排在最前面。比如,在计算 的例子中,中间步骤展示为:4 3 8 1 + 0 7 1 9 0 ( 4 0 0 1 1 ) + 0 0 8 6 6 3, 这里,我们把 分解为 ,分步计算结果为 (即 ,在此过程中我们把这个部分和逆序写成了 ( 4 0 0 1 1 ))加上 。
A.2 小学数学习题
我们以 GSM8K 的训练集(Cobbe 等,2021)作为出发点,运用 GPT-4 的强大功能,生成了一系列类似的数学题目。为了增加题库的丰富度,我们设定了如下的问题模板,并且将温度参数设为 1:
按照所提供例子的 JSON 格式创作 5 道新的数学应用题。
数学应用题例子:
1):{"question": "Meena 为学校的烘培销售烤了 5 打饼干。她卖了 2 打给她的生物老师 Mr. Stone。她的朋友 Brock 买了 7 块饼干,而她的朋友 Katy 则买了 Brock 两倍的量。请问 Meena 还剩多少饼干?","answer": "Meena 总共烤了 5 x 12 = ⟨⟨5*12=60⟩⟩60 块饼干。Mr. Stone 购买了 2 x 12 = ⟨⟨2*12=24⟩⟩24 块饼干。Brock 购买了 7 块,因此 Katy 购买了 2 x 7 = ⟨⟨7*2=14⟩5⟩14 块饼干。总计 Meena 卖出了 24 + 7 + 14 = ⟨⟨24+7+14=45⟩⟩45 块饼干。她剩下的饼干数量是 60 - 45 = ⟨⟨60-45=15⟩⟩15 块。#### 15"}2): […]
3): […]
4): […]
5): […]
类似例子:
6):
每次利用 GPT-4 产生题目时,我们都从 GSM8K 训练集中随机选择了 5 道题目作为样本。这一过程重复了 80k 次,总计创造了 400k 道题目。在此基础上,我们排除了那些 JSON 格式不正确的题目,或是那些中间步骤不能正确引导出最终答案的题目(如上面例子所示,最终的计算结果 ⟨⟨60-45=15⟩⟩ 需要与答案 15 相符,这样的题目才被认为是有效的)。经过这样的筛选,我们得到了包含 379k 道题目的数据集,并为验证过程预留了 1k 道题目。我们使用 GSM8K 的测试集作为我们的测试标准。
在训练明确的“链式推理”(CoT)时,我们采用了自然语言的中间步骤,根据 Wei et al. 的研究(2022b),这种方法比起使用方程式更有效。打个比方,当输入是 Tom 以 200 美元购买了游戏。它们的价值翻了三倍之后,他又卖掉了 40%。他卖游戏赚了多少钱?,它的中间步骤可以表述为 游戏的价值涨到了 200*3=600 美元,因此他通过售出游戏赚到了 600*.4=240 美元。而在训练隐式的“链式推理”教师时,我们只采用方程作为中间步骤,这是基于我们的观察:通常情况下,更多的中间步骤需要更多层次的隐式推理。对于上面的例子,隐式 CoT 的中间步骤简单来说就是:200*3=600,600*.4=240。
附录 B 原始数据结果
| 模型 | #层数 | 4×4 乘法 | 5×5 乘法 | GSM8K-Aug | |||
| 准确率 | 处理速度 | 准确率 | 处理速度 | 准确率 | 处理速度 | ||
| 不含 CoT | |||||||
| GPT-2 小型版 | 12 | 28.7% | 13.2 | 1.2% | 11.1 | 13.3% | 24.7 |
| GPT-2 中型版 | 24 | 76.2% | 7.0 | 1.9% | 5.9 | 17.0% | 13.2 |
| GPT-2 大型版 | 36 | 33.6% | 4.8 | 0.9% | 4.0 | 12.7% | 9.1 |
| ChatGPT | 96 | 2.2% | 1.0 | 0.0% | 1.4 | 28.1% | 1.8 |
| GPT-4 | - | 4.0% | 0.7 | 0.0% | 0.8 | 43.8% | 0.9 |
| 隐式的 CoT | |||||||
| GPT-2 小型版 | 12 | 96.6% | 8.9 | 9.5% | 7.9 | 20.0% | 16.4 |
| GPT-2 中型版 | 24 | 96.1% | 4.8 | 96.4% | 4.3 | 21.9% | 8.7 |
| 明确的 CoT | |||||||
| GPT-2 小型版 | 12 | 100.0% | 2.3 | 100.0% | 1.5 | 40.7% | 2.0 |
| GPT-2 中型版 | 24 | 100.0% | 1.2 | 100.0% | 0.8 | 43.9% | 1.1 |
| GPT-2 Large | 36 | 100.0% | 0.8 | 99.3% | 0.6 | 44.8% | 0.7 |
| ChatGPT | 96 | 42.8% | 0.1 | 4.5% | 0.1 | 61.5% | 0.2 |
| GPT-4 | - | 77.0% | 0.1 | 44.3% | 0.1 | 90.9% | 0.1 |
表 4: 实验数据。这里的准确率 (Acc) 是指完全准确回答问题的能力。吞吐量指的是在单个批次中每秒能处理多少个例子。符号 表明这些数据是基于少量示例提示得出的,而非通过细致调教模型,并且吞吐量是基于 API 调用,这些调用在不同运行中的表现差异很大。
我们在 表 4 中呈现了实验的基础数据。有趣的是,尽管 GPT-4 没有经过连锁思考(Chain of Thought)的特别训练,但它的表现却意外地与经过此类训练的 GPT-2 Large 相媲美,这可能是由于数据泄露或是模型在大规模运作时出现的新能力(参考 Wei et al., 2022a)。
附录 C 少示例提示的基准线
在 表 4,我们用 ChatGPT 和 GPT-4 作为对比标准。对这些标准,我们采取了包含五个示例的少示例提示技术,并设置了温度参数为 0 来实现贪心解码。我们每次会从训练集中随机选取五个示例作为演示。对于算术乘法的数据集,我们保留了原来的数字顺序,并去除了数字间的空白。
在不使用连续输出解题(CoT)的设置下,以下是一个 乘法的示例提示:
请按照示例的格式准确回答最后一个问题。直接给出答案,不需要展开解题过程。
示例问题:
Q: 5646 * 1576
A: #### 08898096Q: 7560 * 3228
A: #### 24403680
待解答的问题:
Q: 1668 * 4380
而在明确需要连续输出解题的情况下, 乘法的示例提示为:
请严格遵循示例的格式回答最后一个问题。不要输出任何额外内容。
示例问题:
Q: 5646 * 1576 A: 1): 6 * 5646 = 33876 (中间和 0 + 33876 = 33876) 2): 70 * 5646 = 395220 (中间和 33876 + 395220 = 429096) 3): 500 * 5646 = 2823000 (中间和 429096 + 2823000 = 3252096) 4): 1000 * 5646 = 5646000 (中间和 3252096 + 5646000 = 8898096) #### 8898096待解答的问题:
Q: 1668 * 4380
附录 D 模型详情
D.1 教师心理解读
在这一环节,对每一个神经网络层级,我们都增添了一个可训练的单层多层感知器(MLP),它基于教师的状态,进而替代对应的学生状态。首先,这个多层感知器通过一个线性层,将教师状态由 的大小映射成 的向量,接着使用 ReLU 函数处理,之后再用另一个线性层将向量大小映射回 。
在实验过程中,我们考察了 值的选择,包括 和一个动态的 值 。结果显示,在解决算术问题时,动态的 值效果最佳。对于 GSM8K 数据集,我们发现对于 GPT-2 小模型, 的效果最好;对于 GPT-2 中等模型, 的效果最佳。
D.2 思维模拟
让我们先从一个更一般的混合方法谈起。在每个层级 ,我们会基于 值先计算出中间步骤中对应的列 。然后定义该层的仿真器隐藏状态为 ,我们利用线性投影技术,将混合分布 的参数设置为与词汇量大小一致(这是因为我们设定了 与中间步骤中相应的单词 相匹配),随后应用 softmax 函数来获取一个有效的概率分布。为了进一步设置函数 的参数,我们将 转换成一个与变压器隐藏层大小 相同的向量,并将这个向量与 结合,然后传递给一个单层多层感知器(MLP)。这个 MLP 在结构上与“教师心理解读”中提到的 MLP 一致,但它使用了一组不同的参数。
在 Vaswani 等人于 2017 年提出的原始 Transformer 架构中,一个层级的隐藏状态会直接成为下一层级的输入。但在这里我们不能这么做,因为那样我们就无法知道具体使用了混合成分中的哪一部分(因为 并不包含 的信息)。因此,我们使用一个函数 来引入有关 的信息,并采用 Hochreiter 和 Schmidhuber 在 1997 年提出的 LSTM 结合自我关注机制来处理这个函数,输出结果将作为下一个 Transformer 层的输入。类似于 Luong 等人在 2015 年的工作,我们首先将 映射成键和查询,然后用 作为查询,通过点式关注机制来关注 ,通过注意力权重计算前面键的加权和。接下来,我们将得到的向量(一般称为上下文向量)与 RNN 的输出结合,通过线性投影把它重新投影成 大小的输出,作为 LSTM 的输出。这个上下文向量还会被添加到 中,作为 LSTM 下一步的输入。最终,我们把 LSTM 的输出传递到下一个 Transformer 层级 。
如果我们不采用混合组件的方法,我们只需在上述过程中将 设为 1。
D.3 结合与优化
在进行结合与优化的步骤时,方法很直接,除了采用了一种混合策略之外。理论上,我们期望在每个层面上选择最可能的混合成分(即最有可能的 token)的 argmax,但问题在于 argmax 函数无法直接进行微分。为了实现完全可微的计算,我们借鉴了 Gumbel-Softmax 方法(参见 Jang 等人,2017;Maddison 等人,2017),采用了一个温度参数来软化 softmax 函数,从而调整各混合组分 的分布:
我们根据这个调整后的分布计算一个加权和 ,这个和是对 的独热编码的加权,接着计算函数 。当这个函数处理 的嵌入时,它会根据权重 对词汇表中的所有嵌入进行加权求和。这个流程可以完全微分,当温度接近零时,我们就能够回到选择 的 argmax 的情况。在我们的实验中,我们把温度设为了一个较低的值,即 0.05。
在处理算术任务时,我们会在结合步骤之后对模拟器和学习者进行微调。但是,在处理 GSM8K 任务时,我们发现即使扩大了数据集,结合后的模型也容易出现过拟合。为了避免这种情况,我们选择固定学习者的参数来减轻过拟合的问题。
附录 E 优化细节
我们采用了 AdamW 算法优化所有模型(参见 Kingma 和 Ba, 2017; Loshchilov 和 Hutter, 2019),设置批量大小为 32,学习率定为 5e-5。对于 的乘法计算,我们对标准模型进行了 30 轮的训练,而在隐式链条推理(CoT)的学生模型训练了 15 轮。在 的乘法计算中,标准模型和学生模型在隐式 CoT 框架下各训练了 40 轮。在 GSM8K 任务中,这两种模型也分别进行了 15 轮的训练。在思维模拟任务上,我们进行了 30 轮训练。而在配对和优化步骤中,无论是 还是 的乘法计算,我们训练了 10 轮;在 GSM8K 任务中则进行了 20 轮训练。
| 真实结果 | 配对优化前预测结果 | 配对优化后预测结果 |
|---|---|---|
| 4*2=8 8*4=32 40-32=8 | 4*2=8 4*8=32 32- initiated=14 | 重写帮助信息:HELPrunnerGreek 第 6 版,inscribedidget 商店改道 – Speedileen 掌握了 victimized648 安装官方 delinqu "# 合法 HELPatin |
| 10*2=20 10+20=30 | 10*2=20 10+20=30 | 重写帮助信息:HELPrunnerGreek 第 6 版,inscribedidget 商店开业 – solderileen 掌握了 According648 PharaohPosarry HELP 楼下 |
| 320+430=750 400+300=700 750+430+400+700=2280 | 320+230=550 340+440=780 300+310=780 384+960=RPG40 | 重写帮助信息:HELPrunnerGreek 感恩 inscribedidget 商店改道 – victimizedileen MOTAccordinglectedileenPos delinqu creat Tamil Rai 概念 |
| 4/2=2 16/2=8 8*2=16 4*16=64 | 16/2=8 8*2=16 16/4=4 | 重写帮助信息:HELPrunnerGreek 感恩,inscribedidget 商店改道 calib solderileen 掌握了 RakousseAcc victimized valuableper565 HELP/ |
表 5: 展现预测的混合组分。我们采用了 GPT-2 Medium 模型,并设置 ,以此来确保每一层 的混合组分对应于 Thought Emulation 步骤中的第 个中间 token。在执行“Couple and Optimize”优化前,该任务在验证集上的准确率是 11.2%,优化后提升至 21.9%。若我们根据映射的混合组分来确定最终答案,在“Couple and Optimize”前后,准确率分别是 9.4% 和 0%。
附录 F 可视化内在推理过程
我们通过中间 tokens 来指导混合组分 的学习,当 时,我们可以把概率最高的混合组分对应回词汇表里的单词,这样就能把推理过程形象化。正如 表 5 展示的,Thought Emulation 步骤完成后、在“Couple and Optimize”步骤进行之前,混合组分与数据中的中间步骤非常相似——这也是我们的训练目标。但是,当我们进一步对耦合系统进行优化之后,混合组分就不再与人类理解的推理步骤相匹配了,这暗示模型的内部推理过程可能与人的思考方式有所不同。
附录 G 更多相关研究
链式思维推理
在研究如何让语言模型处理需要复杂多步骤推理的任务时,有研究者建议训练模型能够明确输出解决问题过程中的每一个步骤(Nye 等人,2021;Sakenis 和 Shieber,2022)。但是随着大规模预训练模型的发展,一些不需此类训练的新方法应运而生。例如,Wei 等人(2022b)就提出了一种通过少量带有中间步骤的示例进行链式思维提示的方法。Kojima 等人(2022)也教导模型在没有任何样本的情况下如何“逐步推理”。其他研究则探讨了更多样的提示数据结构(Yao 等人,2023a;Long,2023;Besta 等人,2023),最优的链式思维提示技巧(Wang 等人,2023;Fu 等人,2023),把链式思维应用于编程(Chen 等人,2022)和 API 使用(Yao 等人,2023b;Schick 等人,2023),乃至在视觉领域也有所应用(Gupta 和 Kembhavi,2023)。尽管如此,这些方法都依赖于详尽的中间步骤,而我们的研究则可以直接输出最终的答案。
自然语言处理的强化学习新探索
在我们的研究中,我们利用了模型的连续隐藏状态来进行逻辑推理。得益于系统的全微分特性,我们使用了梯度下降法来优化模型。我们还探索了一条新路径:允许模型自主构建它们独有的符号推理途径,这些途径可能与人类的思考方式有所不同。我们通过强化学习技术对这些途径进行微调,参考文献包括 Schulman 等人(2017)、Stiennon 等人(2020)等。此外,我们可以根据问题答案的准确度和推理过程的效率来设计奖励机制,这有点像是自动化提示的方法,相关的研究如 Zhou 等人(2023)、Singh 等人(2023)的工作所展示的。